Bit Manipulations

Bit Manipulations

Value range for various bits

8-bit: 0 - 255
16-bit: 0 - 65,535
32-bit: 0 to 4,294,967,295

For signed values:

8-bit: -128 to 127
16-bit: -32,768 to 32,767
32-bit: -2,147,483,648 to 2,147,483,647

Two's Complement:

2 Steps:
1. Negate every bit in the number (For example, 1 is 0000 0001, so it becomes 1111 1110)
2. Add 1. (So, -1 is 1111 1111)

Note: All negative numbers have the MSB (the one at the front) be 1.

Shifting:

Shifting the integer 7 ONCE to the left yields 14 (7*2 is 14)
0000 0111 << 1 = 0000 1110
Logical Shifting the integer 7 ONCE to the right yields 3 (7/2 = 3.5, so, shifting ROUNDS DOWN. Basically, very similar to integer division)
0000 0111 >> 1 = 0000 0011
Arithmetic Shifting the integer requires the MSB to be duplicated for the introduced bit at the front. This is used for negative sign numbers. (Note that it ROUNDS DOWN, as usual, but in this case just dropping the digits after the dot is not enough, since the number is negative.)
1111 0011 (-13) >> 1 = 1111 1001 = -7

Note: Shifting is the fastest possible operation. It takes one tick (or quantum to complete).
So, let's say you have a clock speed of 3.0 GHz. One G is about 10^9. Hertz is equivalent to cycles per second. That amount of shifts can be done per second by such a CPU.
To put it in perspective, addition takes about 5 ticks, multiplication takes about 10, so with 3.0 GHz, only 0.6G additions and 0.3G multiplications per second can be done.
So basically, instead of multiplying by 2 or a power of 2, use shifting. Similarly, if you are dividing by 2 or a power of 2 and can afford truncuation, use shifting.

Bit Manipulators

Shifting is much more useful when used in conjunction with bitwise operators.
Other bitwise operators are:

& (binary) (AND)
| (binary) (OR)
^ (binary) (XOR)
~ (unary) (one's complement or NOT gate for every bit, basically 0 changes to 1, 1 changes to 0)

Note: OR is a plus, except for when OR'ing 1 and 1 (since the result is 1). AND is always a multiplication.

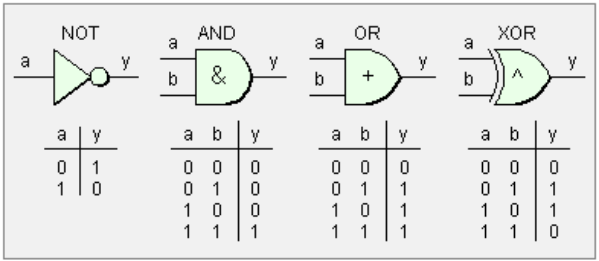
Standard Bit Operations

Note that the letters used aren't chars, they're bits (0 or 1).

Setting a specific bit:



Example:



Explanation:



Clearing a specific bit:



Example:


Explanation:


Testing a specific bit:



Example:



Explanation:

Memory Efficiency while being an Asshole

Depending on the implementation, you sometimes don't know for sure the size of a boolean (in some cases it may even be the size of an int), so optimization using booleans with that may be useless. But, come on, don't use chars for them to make sure they're a byte. “But I can save a couple byt-” No. That's just, well. No.

Though, of course, you can. In fact, you can do one better (or worse, depending on how you look at it): Since chars are 8 bits each, you can fuck with bitwise operators in order to essentially use each bit as a boolean. But you could also use Dvorak and fuck with your teammates who are trying to help you debug your shit. So no.

Memory Efficiency while not Really being an Asshole

Use bitfields.



This whole thing will use up 8 bits.
However, you need to know exactly how many bits you need at compile-time. So, y'know, ehhhhh, no (most of the time, at least).

Another example of Memory Effiency Assholery is using 3 bits instead of 4 bits for compass directions. You normally use 4 bits for north, south, east, west, but there's only 8 directions so you could use 3 bits right? Yeah, if you wanna be an asshole and forget down the line what the fuck north-east is.

Basically, if you're going for a race, do you light your ass on fire to go fast? No? Then don't try to be memory efficient if it requires fucking your future self over.

Masks

Masks are basically testing a single bit, like above. Different label, same shit.

Some Useful Notes on Bitwise Operations:

Generally, when using C++, use hexadecimal when working with bitwise stuff. Binary was included in C++14, so you're stuck with decimal (which is shit for bitwise operations), octal and hex.

Bit-wise operators also have distribution properties:
a&c + b&c = (a+b)&c;
This is pretty useful for optimization.

Swapping values with XOR
#define SWAP(a,b) (((a) ^= (b)), ((b) ^= (a)), ((a) ^= (b)))
Note that macros are literally the spawn of satan.

Also, the compiler does a lot of optimization anyway, mostly with constant values.