pFormulae
Created Thursday 12 May 2016
Distance = Speed * Time
-----
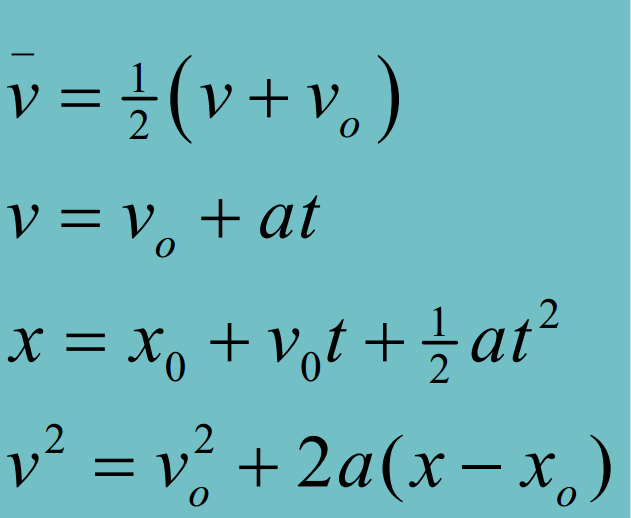
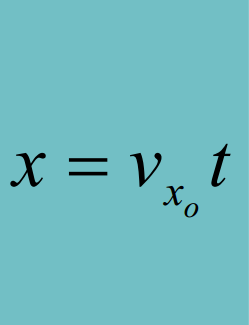
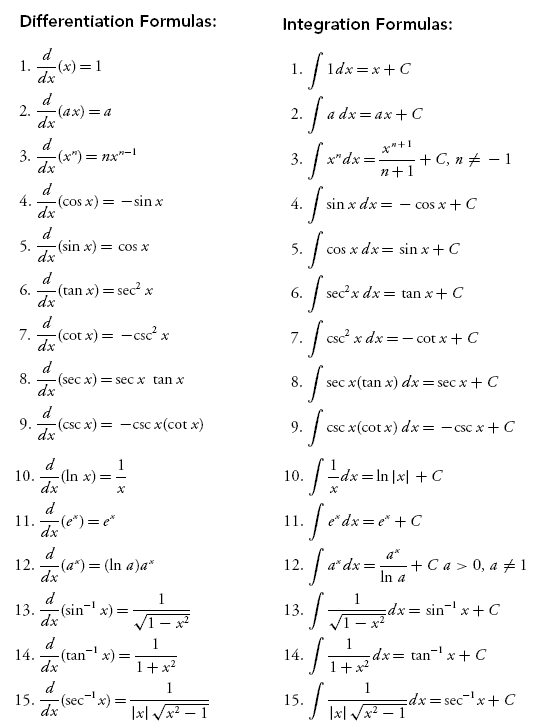
-----
Gravity is -9.80m/s^2
-----
Newton's Laws of Motion
+
First law: When viewed in an inertial reference frame, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a force.[2][3]
Second law: The vector sum of the forces F on an object is equal to the mass m of that object multiplied by the acceleration vector a of the object: F = ma.
Third law: When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.
First law is a SPECIAL CASE of the second law (mass cannot be zero).
----
mass definition. In physics, the property of matter that measures its resistance to acceleration. Roughly, the mass of an object is a measure of the number of atoms in it. The basic unit of measurement for mass is the kilogram.
mass is NOT density. density is mass over volume.
-----
inertia:
a property of matter by which it continues in its existing state of rest or uniform motion in a straight line, unless that state is changed by an external force.
"the power required to overcome friction and the inertia of the moving parts"
-----
Frictional formula gets either static or kinetic friction depending on whether the object in question is moving.
----------
Work Done = Force (direction motion) * distance
If force is perpendicular to displacement then theres no work done
Dot product force with distance to get work done
Fcos(angle)N as y, distance as x = the space under the graph is the work done
hooke's law for springs
work is done BY a force
KE+GPE+EPE = KE+GPE+EPE (- loss)
KE = kinetic energy = 0.5 * m * v^2
GPE = gravitaional potential energy = mgh
EPE = potential energy = 0.5 * k * x^2 where x is displacement from normal length
Hooke's law is a principle of physics that states that the force F needed to extend or compress a spring by some distance X is proportional to that distance. That is: F = kX, where k is a constant factor characteristic of the spring: its stiffness, and X is small compared to the total possible deformation of the spring, F is the force done ON the spring - to get the work EXERTED by the spring make negative.
----------
Power is work done over a certain time interval
P = W/t (J/s) (Watts) = Fdcos(deta)/t = Fvcos(deta) (remember that velocity is d/t)
----------
Linear momentum = mass * velocity (kg.m/s)
Force is the rate of change of momentum F = (delta momentum over delta time)
Total momentum does not change, if no net external force acts on a system
----------
An elastic collision is an encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total kinetic energy before the encounter. Elastic collisions occur only if there is no net conversion of kinetic energy into other forms (such as heat or noise).
----------
Momentum can have direction ( can be negative )
coefficient of restitution = -(VA prime - VB prime) / (VA - VB)
elastic COR = 1
nonelastic COR = 0
COR = ratio of impulses
--------------------
Work required to stretch a spring can be obtained by integrating force formula at original position and minusing the integrationp of the force formula at end position
RELATED work done is equal to change in kinetic energy
----------
Equilibrium = net force is 0
rigidbody moving around just has center of mass as a projectile motion with no rotation (https://www.youtube.com/watch?v=DY3LYQv22qY&gl=SG&hl=en-GB)
----------
v=R * angular velocity
a(tan) -> a(tangential) = centripetal
a(R) = centrifugal
----------
A force is conservative if:
the work done by the force on an object moving from
one point to another depends only on the initial and
final positions of the object, and is independent of the
particular path taken.
Another definition of a conservative force:
a force is conservative if the net work done by the force
on an object moving around any closed path is zero
Potential energy can
only be defined for
conservative forces.


---------- ther
Which to use for solving problems?
- Newton’s laws: best when forces are constant
- Work and energy: good when forces are constant; also
--------
Force = change in momentum over change in time
----------
10:06 PM - Chaoclypse: energy -> joules
10:06 PM - Chaoclypse: force -> newtons
10:06 PM - Chaoclypse: momentum -> kg m/s (wtf)
10:06 PM - Chaoclypse: torque -> Nm
----------
Getting center of mass

Backlinks: index:PHY200 Notes